Overview
This project focuses on developing advanced sparse modeling and visualization techniques for geometric transformation fields, an extension of vector fields that represent geometric transformations at each point.
Background and Goal
The Kyoto Collection of Human Embryo stored at the Congenital Anomaly Research Center, Graduate School of Medicine, Kyoto University is one of the precious and most unique collections in the world.
While serial tissue sections allow detailed observation of organogenesis under a microscope, it is difficult to determine the original three-dimensional shape of a single specimen because it is spread into hundreds of sections. In addition, physical distortion occurs in the sectioning processes, and the original three-dimensional shape cannot be restored by simply stacking digitized section images.
Therefore, this study addresses the issue of restoring the original 3D shape by compensating for the physical distortion.
The process of human development is still unknown.
- Major organs have developed two months after fertilization (usually complete by the time pregnancy is detected).
- Development processes occur in the body and are difficult to observe.
Serial section specimen of human embryo
- Produced about 50 years ago; new collection is difficult.
- ✓ Easy to discriminate organs and tissues in detail using microscopy.
- ✗ Difficulty in understanding 3D morphology.
- 3D reconstruction from serial sections
- ● Hundreds of sections or more from a single specimen
- ● Physical distortion occurs during sectioning
Approach
To cope with large deformations, we took a feature-based approach that estimates the keypoint matches between image pair. The problem is to estimate the deformation field caused by sectioning from the keypoint matches.
In general, only a small number of keypoint matches are obtained, and accurate estimation of the deformation field is not trivial. In this study, we focus on "geometric transformations" that can be estimated from several keypoint matches obtained in a local region.
Instead of the vector field representation, we considered the field of geometrical transformations that change smoothly in space as a latent mathematical structure in real space, and work on its modeling. For example, by using similarity transformations and rigid transformations, geometric properties such as isotropy and isometry are expected to be preserved.
Method
This project aims to develop sparse modeling techniques to model geometric transformation fields in a data-driven manner from a small number of samples.
Only multiplicative operations are allowed for geometric transformations to preserve their geometric properties. Since conventional sparse modeling methods are formulated based on additive operations, if applied as is, the geometric properties of geometric transformations are lost. For example, linear combination of geometric transformations should be formulated according to Lie algebra.
Therefore, we extend the conventional sparse modeling according to the Lie algebra and reformulate it to fit the Lie group, which geometric transformations belongs to. We also developed a method to optimize the entire registration of hundreds of serial sections to minimize the deformation in each image, and to reconstruct the original 3D shape.
We have developed a new method that enables us to understand the morphological changes from limited information, and demonstrated its effectiveness for a wide range of objects from medical image processing to meteorological data.
Theory
A new analysis method that can express complex deformations from limited samples by changing the focus from "point to point" to "region to region".
When trying to estimate the deformation of all pixels from a small number of keypoint matches, the coordinates of the red dots are the same in Figures A - C and Figures A' - C'. The conventional vector field, which captures changes from "point to point" cannot distinguish them.
However, focusing on the region around the red dots, it can be seen that the rotation is different in Figures B and C. By using a method that captures changes from "region to region", it is possible to express the transformation of all A to C differently.
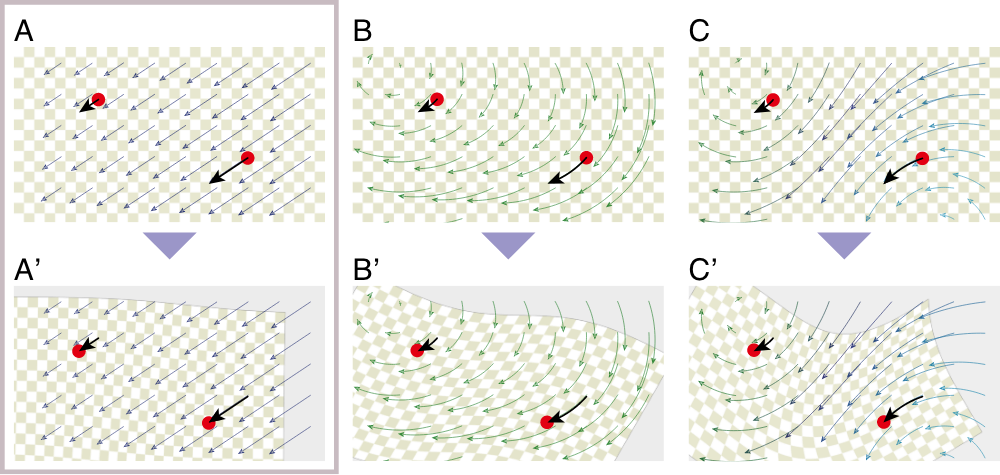
Conventional method: Vector field
"Point-to-Point": Represent the displacement as a vector.
Displacement＝translation
\( x + dx \) : Addition.
A-C cannot be distinguished from the samples.
Our method: geometric transformation field
"Region-to-Region": Represent the displacement as a geometric transformation.
Geometric transformation
Rigid/Similarity transformation
translation &rotation, scaling
\( qx \) : Multiplication.
A, B and C can be expressed differently from the samples.
Developed methods for Geometric Transformation Fields
-
Sparse Regression
-
Graph Optimization
-
Spectral Analysis
Results
We were able to reconstruct the 3D shape of a human embryo from hundreds of serial sections produced more than 50 years ago.
Result 1: Non-rigid Registration of Image Pair
Sparse Regression2D rigid transformations
Derive the deformation field from sparse keypoint matches in an image pair.
Result 2: 3D Reconstruction from Serial Sections
Graph Optimization2D rigid transformations
We perform global optimization of the non-rigid registration for hundreds of serial sections to reconstruct a 3D model while minimizing distortions in each slice.
Applications
Demonstrated effectiveness in analyzing deformations in various applications from medical image processing to meteorological data.
Application 1: Advection Modeling on Globe
Sparse Regression3D rotations
Estimating the global advection from the cloud motion observed from satellite images.
Application 2: Registration of CT images
Sparse Regression3D similarity transformations
Estimating the lung deformation between inspiration and expiration.
Future Prospects
- Integration with deep learning techniques, other statistical analysis, and signal processing techniques.
- Investigating the guideline for the selection of geometric transformation class (rigid/similarity transformations, etc.) according to the application target.
- Exploring other applications.